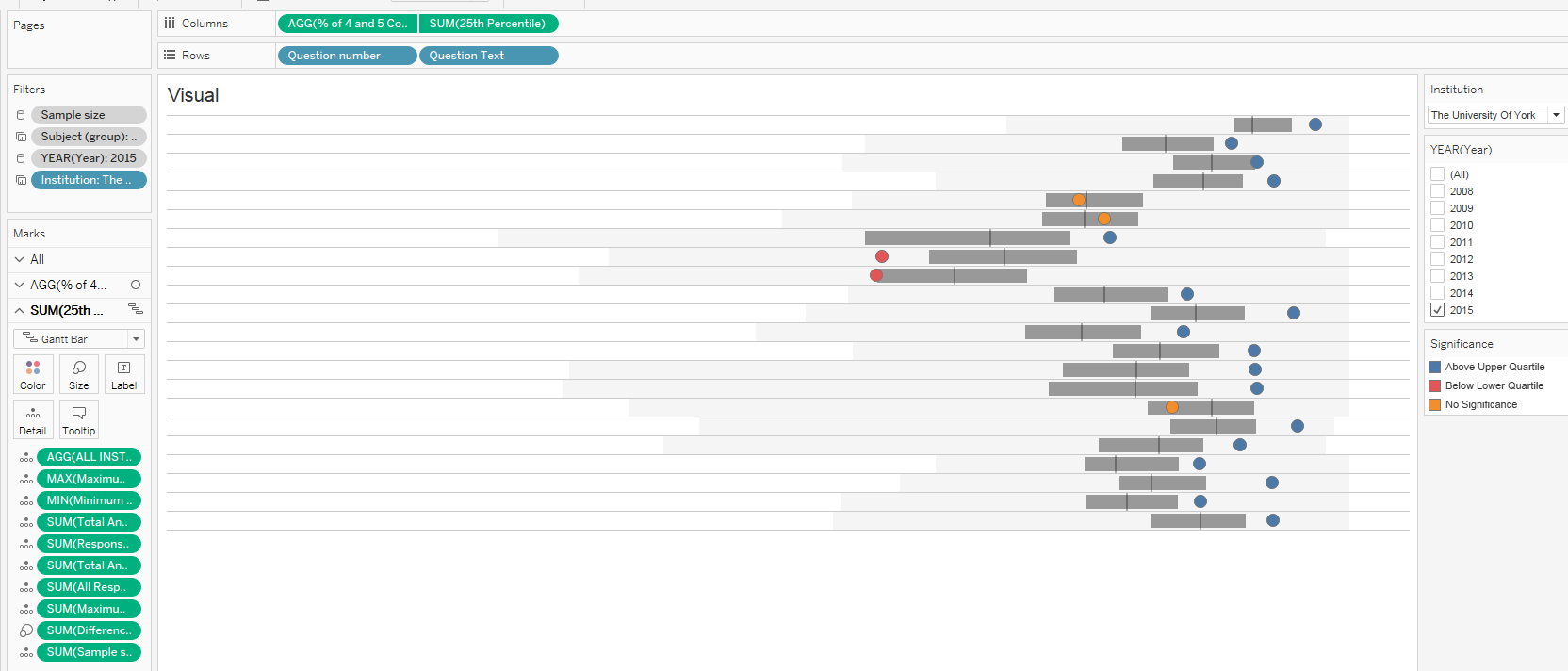
The Workout Wednesday for week 24 is a great way to represent where a result for a particular value falls with respect to a broader collection. I’ve used a spine chart recently on a project where most data was centered around certain points and I wanted to show the range. Propagating maximums, minimums, averages, quartiles, and (when appropriate) medians can help to profile data very effectively.
So I started off really enjoying where this visualization was going. Also because the spine chart I made on a recent project was before I even knew the thing I developed had already been named. (Sad on my part, I should read more!)
My enjoyment turned into caution really quickly once I saw the data set. There are several ratios in the data set and very few counts/sums of things. My math brain screams trap! Especially when we start tiptoeing into the world of what we semantically call “average of all” or “overall average” or something that somehow represents a larger collective (“everybody”). There is a lot of open-ended interpretation that goes into this particular calculation and when you’re working with pre-computed ratios it gets really tricky really quickly.
Here’s a picture of the underlying data set:
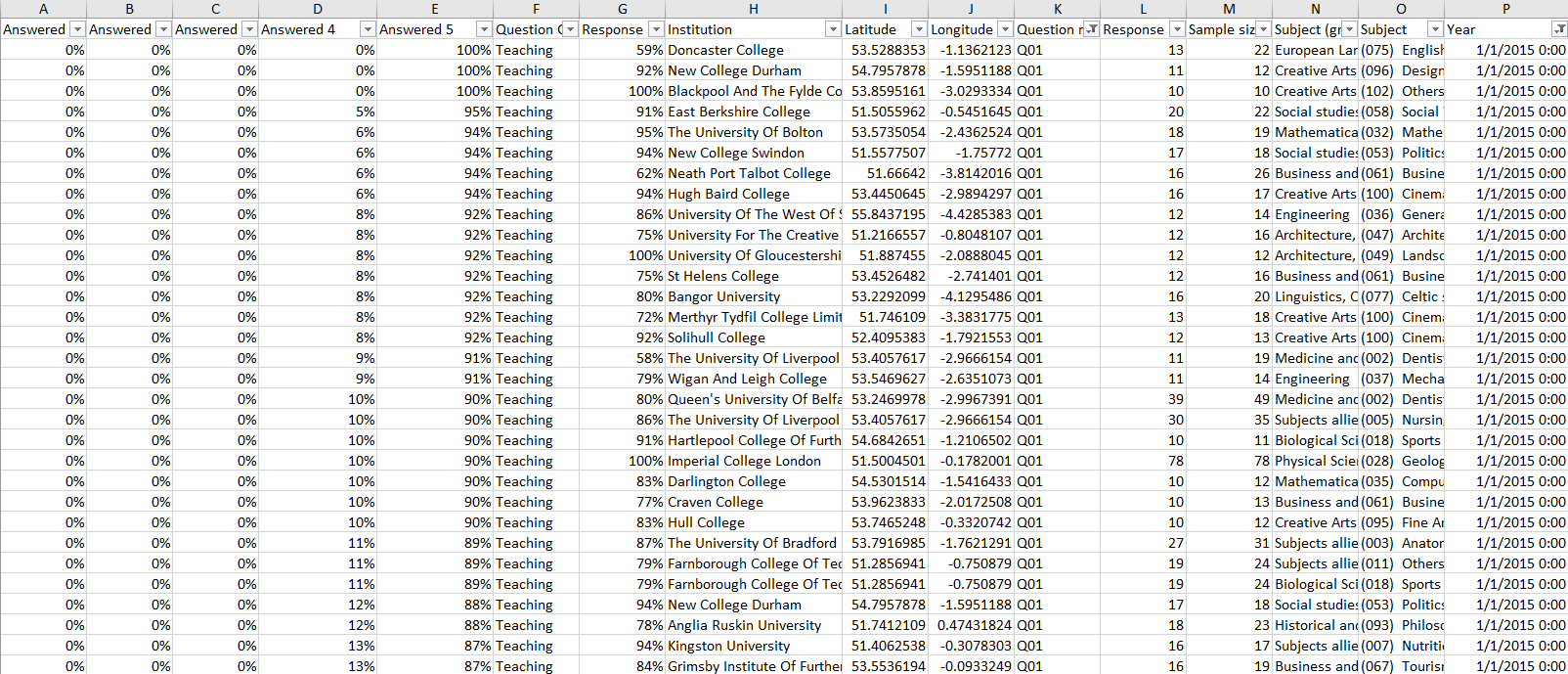
Some things to notice right away – the ratios for each response are pre-computed. The number of responses is different for each institution. (To simplify this view, I’m on one year and one question).
So the heart of the initial question is this: if I want to compare my results to the overall results, how would I do that? Now there are probably 2 distinct camps here. 1: take the average of one of the columns and use that to represent the “overall average”. Let’s be clear on what that is: it is the average pre-computed ratio of a survey. It is NOT the observed percentage of all individuals surveyed. That would be option 2: the weighted average. For the weighted average or to calculate a representation of all respondents we could add up all the qualifying respondents answering ‘agree’ and divide it by the total respondents.
Now we all know this concept of average of an average vs. weighted average can cause issues. Specifically we’d feel the friction immediately if there were several low-end responses commingled with several higher response capturing entities. EX: Place A: 2 people out of 2 answered yes (100%) and Place B: 5 out of 100 answered ‘yes’ (5%). If we average 100% and 5% we’ll get 52.5%. But what if we take 7 out of 102, that’s 6.86% – a way different number. (Intentionally extreme example.)
So my math brain was convinced that the “overall average” or “ratio for all” should be inclusive of the weights of each Institution. That was fairly easy to compensate for: take each ratio and multiply it by the number of respondents to get raw counts and then add those all back up together.
The next sort of messy thing to deal with was finding the minimums and maximums of these values. It seems straightforward, but when reviewing the data set and the specifications of what is being displayed there’s caution to throw with regard to level of aggregation and how the data is filtered. As an example, depending on how the ratios are leveraged, you could end up finding the minimum of 3 differently weighted subjects to a subject group. You could also probably find the minimum Institution + subject result at the subject level of all the subjects within a group. Again I think the best bet here is to tread cautiously over the ratios and get into raw counts as quickly as possible.
So what does this all mean? To me it means tread carefully and ask clear questions about what people are trying to measure. This is also where I will go the distance and include calculations in tool tips to help demonstrate what the values I am calculating represent. Ratios are tricky and averaging them is even trickier. There likely isn’t a perfect way to deal with them and it’s something we all witness consistently throughout our professional lives (how many of us have averaged a pre-computed average handle time?).
Beyond the math tangent – I want to reiterate how great a visualization I think this is. I also want to highlight that because I went deep-end math on it that I decided to go deep end development different.
The main difference from the development perspective? Instead of using reference bands, I used a gannt bar as the IQR. I really like using the bar because it gives users an easier target to hover over. It also reduce some of the noise of the default labeling that occurs with reference lines. To create the gannt bar – simply compute the IQR as a calculated field and use it as the size. You can select one of the percentile points to be the start of the mark.